2025
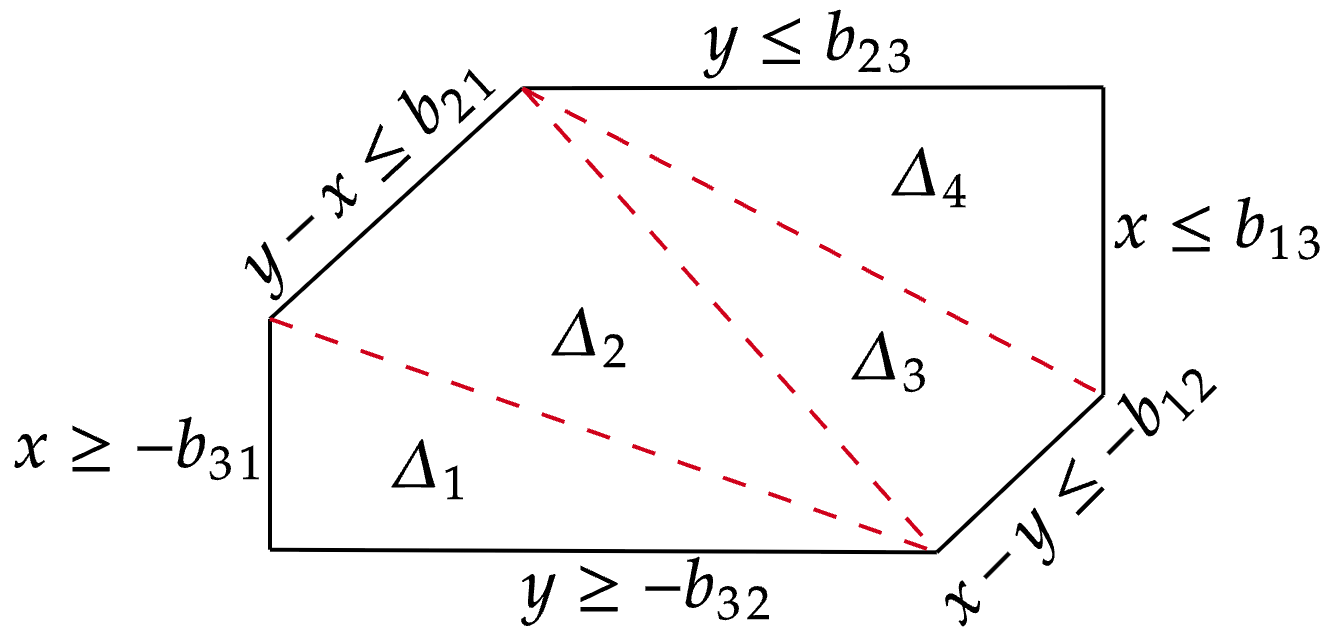
Computing parametric weighted Ehrhart polynomial of smooth polytopes
Daniel Hwang, Juliet Whidden, Josephine Yu
Submitted to Formal Power Series and Algebraic Combinatorics (FPSAC) 2026 Spotlight
We show that when integral polytopes are deformed while keeping the same facet normal vectors, the coefficients of weighted Ehrhart and h* polynomials are piecewise polynomial functions in the ``right-hand sides" of the linear inequalities defining the polytopes. We give an algorithm and an implementation in SageMath for computing these polynomials for smooth polytopes, such as type A alcoved polytopes, using a weighted Euler-Maclaurin type formula by Khovanskii and Pukhlikov.
Computing parametric weighted Ehrhart polynomial of smooth polytopes
Daniel Hwang, Juliet Whidden, Josephine Yu
Submitted to Formal Power Series and Algebraic Combinatorics (FPSAC) 2026 Spotlight
We show that when integral polytopes are deformed while keeping the same facet normal vectors, the coefficients of weighted Ehrhart and h* polynomials are piecewise polynomial functions in the ``right-hand sides" of the linear inequalities defining the polytopes. We give an algorithm and an implementation in SageMath for computing these polynomials for smooth polytopes, such as type A alcoved polytopes, using a weighted Euler-Maclaurin type formula by Khovanskii and Pukhlikov.
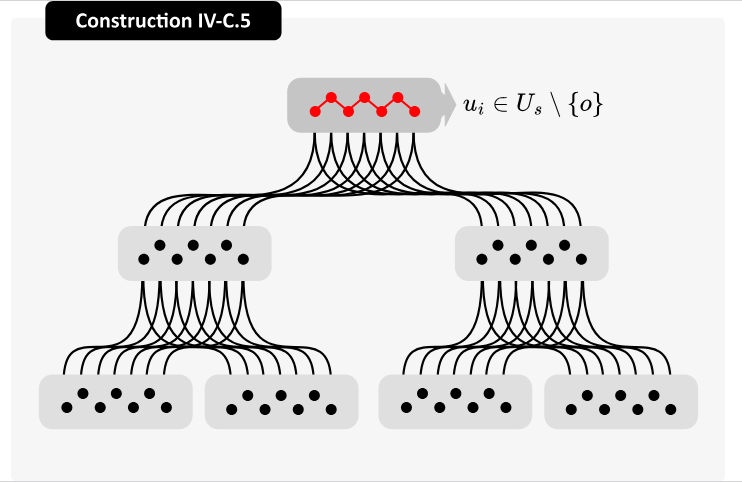
Edge-Disjoint Spanning Trees on Star-Product Networks
Kelly Isham*, Laura Monroe*, Kartik Lakhotia*, Aleyah Dawkins, Daniel Hwang, Ales Kubicek (* equal contribution)
International Parallel and Distributed Processing Symposium (IPDPS) 2025
Resulting publication of Summer 2024 internship completed at Los Alamos National Laboratory under Laura Monroe. We investigate a generalization of the Cartesian product on graphs called the star product and under certain conditions, carefully construct a maximal number of edge-disjoint spanning trees on it. Star products on graphs are ideal for network topologies, as they have low diameter, high scalability, and as our work shows, high parallelism.
Edge-Disjoint Spanning Trees on Star-Product Networks
Kelly Isham*, Laura Monroe*, Kartik Lakhotia*, Aleyah Dawkins, Daniel Hwang, Ales Kubicek (* equal contribution)
International Parallel and Distributed Processing Symposium (IPDPS) 2025
Resulting publication of Summer 2024 internship completed at Los Alamos National Laboratory under Laura Monroe. We investigate a generalization of the Cartesian product on graphs called the star product and under certain conditions, carefully construct a maximal number of edge-disjoint spanning trees on it. Star products on graphs are ideal for network topologies, as they have low diameter, high scalability, and as our work shows, high parallelism.
2022

Analyzing the bistability of the minimally bistable ERK network using the discriminant locus
Daniel Hwang
Senior Thesis 2022
Senior thesis (completed as part of the PRUV Program) submitted for Graduation with Distinction, advised by Margaret Regan. This project utilized homotopy continuation, a technique from numerical algebraic geometry, to distinguish different regions of parameters of a parameterized polynomial system that yield different numbers of real positive steady states of the minimally bistable ERK network.
Analyzing the bistability of the minimally bistable ERK network using the discriminant locus
Daniel Hwang
Senior Thesis 2022
Senior thesis (completed as part of the PRUV Program) submitted for Graduation with Distinction, advised by Margaret Regan. This project utilized homotopy continuation, a technique from numerical algebraic geometry, to distinguish different regions of parameters of a parameterized polynomial system that yield different numbers of real positive steady states of the minimally bistable ERK network.